On this post I will show a mini project I have been working on for the last few days. The goal is generate boolean or binary data from
categorical data. For doing so, I will primarly use Pandas and Numpy libraries. This class was created for testing purposes, so performance has not been taken into account and therefore is not relevant at this moment, however I am convinced that the code can be much more optimized.
Firstly, a short explanation about what this code is doing:
The next table represents the input data, as shown, fields p1, p2, p3 and p4 store categorical data, in this case a product code. Each module consists of four products (p) at most. Note: field "modules" is the index (row names).
Now, let's imagine we want to solve a linear equation system (Ax = b) composed by field p1, p2, p3 and p4 as matrix "A" , unknows (A1, A2, A3, A4, B1, B2, C1) and price as vector "b":
$A=\begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{m1} & a_{m2} & \cdots & a_{mn}\end{bmatrix}, \quad x=\begin{bmatrix}x_1 \\x_2 \\\vdots \\x_n\end{bmatrix}, \quad b=\begin{bmatrix}b_1 \\b_2 \\\vdots \\b_m\end{bmatrix}$
The matrix equations shows that size(A) = m x n, size(x) = n and size(b) = m. On the above example columns(A) is not equal to size(x). Hence, we need a new matrix A with the correct shape, see below.
$A=\begin{bmatrix}1 & 1 & 0 & 0 & 0 & 0 & 0 \\1 & 0 & 1 & 0 & 0 & 0 & 0 \\0 & 0 & 0 & 1 & 1 & 1 & 1 \\1 & 0 & 0 & 0 & 1 & 0 & 1 \end{bmatrix}, \quad x=\begin{bmatrix}A1 \\A2 \\A3 \\A4 \\B1 \\B2 \\C1 \end{bmatrix}, \quad b=\begin{bmatrix}9.90 \\10.50 \\20.30 \\22.10 \end{bmatrix}$
If we get a matrix "A" like the previous one, then we can solve the system easier.
Using vectorial notation, m_1 = A(1, :).x (e.g. Matlab indexing)
Before we continue, I would like to remark that the above system can be easily solvead by isolating x from the equation or by using LU decomposition, especially for square matrices. When dealing with non square matrices ($m \neq n$) the next methods are normaly used:
Code:
The code tries to be self-explanatory, however I consider that three functions need more details:
Below a short example using the class CatBin:
Hence, having large amount of binary data in a database can also have an impact on performance, so I will not recommend to store the new dataset in a DB better create a system file. There are other options of storing a sparse matrix much more efficient that save the complete data in a DB (CSR or CSC, for instance).
One more example: This dataset includes extra columns before and after the fields with categorical data (2194 x 13). If the order of the extra columns matters is convenient to use ordered dictionaries.
That's all for this post, I hope you find it useful.
Firstly, a short explanation about what this code is doing:
The next table represents the input data, as shown, fields p1, p2, p3 and p4 store categorical data, in this case a product code. Each module consists of four products (p) at most. Note: field "modules" is the index (row names).
| modules | p1 | p2 | p3 | p4 | price |
|---|---|---|---|---|---|
| m_1 | A1 | A2 | 9.90 | ||
| m_2 | A1 | A3 | 10.50 | ||
| m_3 | B1 | B2 | A4 | C1 | 20.30 |
| m_4 | B1 | A1 | C1 | 22.10 |
Now, let's imagine we want to solve a linear equation system (Ax = b) composed by field p1, p2, p3 and p4 as matrix "A" , unknows (A1, A2, A3, A4, B1, B2, C1) and price as vector "b":
$A=\begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{m1} & a_{m2} & \cdots & a_{mn}\end{bmatrix}, \quad x=\begin{bmatrix}x_1 \\x_2 \\\vdots \\x_n\end{bmatrix}, \quad b=\begin{bmatrix}b_1 \\b_2 \\\vdots \\b_m\end{bmatrix}$
The matrix equations shows that size(A) = m x n, size(x) = n and size(b) = m. On the above example columns(A) is not equal to size(x). Hence, we need a new matrix A with the correct shape, see below.
$A=\begin{bmatrix}1 & 1 & 0 & 0 & 0 & 0 & 0 \\1 & 0 & 1 & 0 & 0 & 0 & 0 \\0 & 0 & 0 & 1 & 1 & 1 & 1 \\1 & 0 & 0 & 0 & 1 & 0 & 1 \end{bmatrix}, \quad x=\begin{bmatrix}A1 \\A2 \\A3 \\A4 \\B1 \\B2 \\C1 \end{bmatrix}, \quad b=\begin{bmatrix}9.90 \\10.50 \\20.30 \\22.10 \end{bmatrix}$
If we get a matrix "A" like the previous one, then we can solve the system easier.
Using vectorial notation, m_1 = A(1, :).x (e.g. Matlab indexing)
Before we continue, I would like to remark that the above system can be easily solvead by isolating x from the equation or by using LU decomposition, especially for square matrices. When dealing with non square matrices ($m \neq n$) the next methods are normaly used:
- Normal equation: $x = (A^{T} A)^{-1} A^{T} b $
- QR factorization
- SVD decomposition
Code:
import numpy as np
import pandas as pd
import warnings
import matplotlib.pyplot as plt
class CatBin(object):
def __init__(self, i_file, o_file=False, cat_cols="all", other_cols=None, op_nan=True):
"""
Class to convert a matrix with categorical data into a matrix with binary data.
Example: Convert the below matrix into a binary matrix
initial_data =
modules p1 p2 p3 p4 price
m_1 A1 A2 nan nan 9.90
m_2 A1 nan A3 nan 10.50
m_3 B1 B2 A4 C1 20.30
m_4 B1 nan A1 C1 22.10
binary_data =
modules A1 A2 A3 A4 B1 B2 C1 price
m_1 1 1 0 0 0 0 0 9.90
m_2 1 0 1 0 0 0 0 10.50
m_3 0 0 0 1 1 1 1 20.30
m_4 1 0 0 0 1 0 1 22.10
Uses:
Solve a linear equation system: Ax = b
A = matrix[0,1]
x = [A1, A2, A3, A4, B1, B2, C1]
b = price
Note:
if non-square matrix, we can solve the system by using some
of the well-known methods:
Normal equation
QR factorization
SVD decomposition
Graphs - adjacency matrix - connectivity
...
:param i_file: input_file in csv format
:param o_file: if True a csv is generated. The path must be provided.
:param cat_cols: slicing - e.g [1, 10] -> from column 1 to 10(not included - pandas)
:param other_cols:
if the new data frame must preserve others columns besides those
with categorical data, position and name should be provided in a dictionary.
e.g
others = {'i' : 'modules', 'e', 'prices'}
if 'i', that column will be inserted on the first position in the new data frame
data.insert(0, 'name', column_data)
if 'e', that column will be inserted after the rest of columns
data['name'] = column_data
:param op_nan: if true all NaN values will be removed.
"""
self.o_file = o_file
self.cat_cols = cat_cols
self.other_cols = other_cols
self.nan = op_nan
self.list = []
self.rows = None
self.columns = None
self.p_sparsity = -1
self.input_data = pd.read_csv(i_file)
self.boolean_m = None
self.boolean_a = None
if self.cat_cols is "all":
if self.nan is True:
# if all data is categorical data to be converted, automatically
# others_cols must be false to avoid inconsistencies.
self.data = self.input_data.fillna(value='nan')
else:
self.data = self.input_data
if other_cols is not None:
other_cols = None
warnings.warn("other_cols has been set to False to avoid inconsistencies")
else:
# cat_cols is an array [start, end]
if isinstance(self.cat_cols, list):
if len(self.cat_cols) == 2:
_start = self.cat_cols[0]
_end = self.cat_cols[1]
if self.nan is True:
self.data = self.input_data.fillna(value='nan').iloc[:, _start: _end]
else:
self.data = self.input_data.iloc[:, _start, _end]
else:
raise ValueError("'start'and 'end' position must be provided")
else:
raise TypeError("cat_cols is not a list")
if not self.data.empty:
# extract unique values:
self.list = self.unique_values()
else:
raise ImportError("errors or empty csv file. Check input file")
def unique_values(self):
""" return sorted list of unique values """
u_values = pd.Series(self.data.values.ravel()).unique()
if self.nan is True:
return np.sort(u_values[u_values != 'nan'])
else:
return np.sort(u_values)
def boolean_matrix(self):
matrix = []
for i in range(len(self.data)):
v = self.data.iloc[i, :].values
# avoid worrying about the argument op_nan
intersect = set(v).intersection(self.list)
ea = np.zeros(len(self.list))
for n in intersect:
for index, v in enumerate(self.list):
if n == v:
ea[index] = 1
matrix.append(ea)
self.rows = len(matrix)
self.columns = len(matrix[0])
self.boolean_m = pd.DataFrame(matrix, columns=self.list)
return self.boolean_m
def boolean_augmented_matrix(self):
"""
The goal of this function is create the augmented matrix:
Ax = b --> augmented_matrix = [A|b]
However, this function allows the option of inserting at least
one first column and many others columns after the boolean data,
in case that was required to suit your necessities.
"""
if self.cat_cols is not 'all':
if self.boolean_m is None:
self.boolean_a = self.boolean_matrix()
else:
self.boolean_a = self.boolean_m.copy()
if self.other_cols is not None and isinstance(self.other_cols, dict):
for key, value in self.other_cols.items():
if key[0] is 'i':
self.boolean_a.insert(0, value, self.input_data[value])
elif key[0] is 'e':
self.boolean_a[value] = self.input_data[value]
else:
raise ValueError("Incorrect key format")
else:
warnings.warn("insufficient arguments")
return self.boolean_a
else:
raise ValueError("cat_cols = 'all' the aug. matrix is not possible")
def sparsity(self):
"""
The sparsity or density is the fraction of non-zero elements in a matrix.
:return: ratio non-zero/total
"""
if self.rows and self.columns and self.boolean_m is not None:
total = self.rows * self.columns
non_zeros = sum(self.boolean_m[self.boolean_m == 1].count())
self.p_sparsity = non_zeros / total
return "sparsity = {0:.4}%".format(self.p_sparsity * 100)
else:
raise ValueError("incorrect data shape. A boolean transformation is required")
def generate_csv(self, matrix_type='normal'):
"""
generate a csv file with boolean matrix or augmented matrix
note: removes first column (index)
"""
if matrix_type in ['normal', 'augmented']:
if matrix_type is 'normal':
if self.boolean_m is not None:
self.boolean_m.to_csv(self.o_file, index=False)
else:
if self.boolean_a is not None:
self.boolean_a.to_csv(self.o_file, index=False)
else:
raise ValueError("select: normal or augmented")
@property
def clean_data(self):
return self.data
@property
def raw_data(self):
return self.input_data
@property
def initial_size(self):
""" Only includes those fields with categorical data"""
rows = self.data.shape[0]
columns = self.data.shape[1]
return "rows={0}, columns={1}, total={2} elements".\
format(rows, columns, rows * columns)
@property
def final_size(self):
rows = self.boolean_m.shape[0]
columns = self.boolean_m.shape[1]
return "rows={0}, columns={1}, total={2} elements".\
format(rows, columns, rows * columns)
The code tries to be self-explanatory, however I consider that three functions need more details:
- boolean_matrix: This function contains the basic code to convert the input data. Basically, it compares each row from the initial data "A" with its unique values and inserts one on those positions where matching. As example, this task can be done in Matlab much easier, Matlab can compare two arrays with different length by using the function "ismember()":
p = {'A1', 'A2', 'A3', 'A4', 'B1', 'B2', 'C1'}; % character arrays or cell arrays p_test = {'A1', 'B1','C1'}; ismember(p, p_test) ans = 1 0 0 0 1 0 1 - boolean_augmented_matrix: The augmented matrix is that obtained by appending the solution vector "b" to matrix "A", usually denoted as [A b] or (A|b). Having a solvable linear equation system, then the augmented matrix [A b] has the same rank as A. Besides of creating the augmented matrix, this function allows the possibility to append other columns if needed.
- Sparsity: The sparsity or density is the fraction of non-zero elements in matrix. A typical example of sparse matrix is the adjacency matrix of an undirected graph.
Below a short example using the class CatBin:
from others.catbin import CatBin
import time
file = "test data/i_simple.csv"
output_file = "test data/clean_matrix.csv"
others = {'i': 'modules', 'e': 'price'}
t1 = time.time()
ct = CatBin(i_file=file, o_file=output_file, cat_cols=[1, 5], other_cols=others, op_nan=True)
unique_v = ct.unique_values()
boolean_m = ct.boolean_matrix()
boolean_a = ct.boolean_augmented_matrix()
sparsity = ct.sparsity()
t = time.time() - t1
print(t)
print(ct.initial_size)
print(ct.final_size)
ct.generate_csv()
The file "i_simple.csv" is exactly the first table on this post. This code uses all features of the class, producing both boolean matrix and boolean augmented matrix and calculates the sparsity ratio. The most simple example needs 5 lines (without verbose).
from others.catbin import CatBin
file = "test data/i_simple.csv"
output_file = "test data/clean_matrix.csv"
ct = CatBin(i_file=file, o_file=output_file, cat_cols=[1, 5],
other_cols={'i': 'modules', 'e': 'price'}, op_nan=True)
boolean_a = ct.boolean_augmented_matrix()
Results:
modules A1 A2 A3 A4 B1 B2 C1 price
0 m_1 1 1 0 0 0 0 0 9.9
1 m_2 1 0 1 0 0 0 0 10.5
2 m_3 0 0 0 1 1 1 1 20.3
3 m_4 1 0 0 0 1 0 1 22.1
0.010005950927734375
rows=4, columns=4, total=16 elements
rows=4, columns=7, total=28 elements
In my laptop(4GB, i5) the process took 0.01 seconds. The next step will be to test something bigger. The dimensiones of the new data is 2194 x 11:
1.1577680110931396
rows=2194, columns=9, total=19746 elements
rows=2194, columns=294, total=645036 elements
Due to the number of unique values is much higher, the number of elements is almost 650.000 and the process now took 1.15 seconds, surely this can be improved, but for now it works for my purposes. As shown, the new dimensiones will be multiplied by a factor X(unique values / initial columns).Hence, having large amount of binary data in a database can also have an impact on performance, so I will not recommend to store the new dataset in a DB better create a system file. There are other options of storing a sparse matrix much more efficient that save the complete data in a DB (CSR or CSC, for instance).
One more example: This dataset includes extra columns before and after the fields with categorical data (2194 x 13). If the order of the extra columns matters is convenient to use ordered dictionaries.
from others.catbin import CatBin
from collections import OrderedDict
import time
file = "test data/i_data_2.csv"
output_file = "test data/clean_matrix.csv"
others = {'i1': 'modules', 'i2': 'modules2', 'e1': 'price', 'e2': 'price2'}
ordered_others = OrderedDict(sorted(others.items(), key=lambda t: t[0]))
t1 = time.time()
ct = CatBin(i_file=file, o_file=output_file, cat_cols=[2, 11],
other_cols=others, op_nan=True)
boolean_m = ct.boolean_matrix()
boolean_a = ct.boolean_augmented_matrix()
t = time.time() - t1
sparsity = ct.sparsity()
print(t)
print(ct.initial_size)
print(ct.final_size)
print(boolean_a)
Finally, a function for plotting:
def plot_sparse(self, ticks=False, x_ticks=False, y_ticks=False, y_label=None,
sparsity=False):
"""
Notes:
if sparsity was previously calculated - this figure can be included.
if data is extraordinarily large might be convenient to hide ticks.
"""
if sparsity and self.p_sparsity >= 0:
plt.title("sparsity ratio = {0:.4}%".format(self.p_sparsity * 100), fontsize=10)
plt.suptitle("boolean matrix", fontsize=14, fontweight='bold')
else:
plt.title("boolean matrix", fontsize=14, fontweight='bold')
plt.imshow(self.boolean_m, interpolation='nearest', cmap='gist_yarg')
if ticks is True:
plt.yticks(range(self.boolean_m.shape[0]))
if x_ticks is True:
plt.xticks(np.arange(len(self.list)), self.list)
if y_label is not None and y_ticks is True:
plt.yticks(np.arange(len(self.input_data[y_label])), self.input_data[y_label])
else:
plt.axis('off')
plt.show()
Let's plot both matrices used on the previous examples:
ct.plot_sparse(ticks=True, x_ticks=True, sparsity=True)
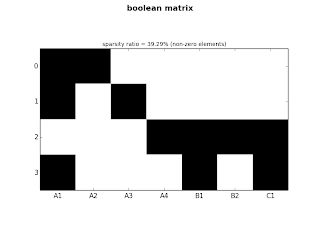 |
| fig.1: small matrix |
ct.plot_sparse(ticks=False, sparsity=True)
 |
| fig.2: medium matrix |
ct.plot_sparse(ticks=True, x_ticks=True, sparsity=True)
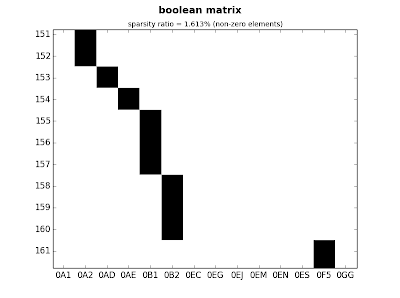 |
| fig.3: medium matrix - detail |